\(0<x<1\) かつ \(x^2+\frac{1}{x^2}=7\) のとき \(x-\frac{1}{x}\) の値を求めよ。
式の値を求める問題です。
数Ⅰの始めの単元なので、高校生になって間もない人も見たことがある問題でしょう。
\((x-\frac{1}{x})^2=x^2-2+\frac{1}{x^2}\)
\(=7-2\)
\(=5\)
よって \(x-\frac{1}{x}=\pm\sqrt5\)
ここで \(0<x<1\) であるから \(x<\frac{1}{x}\)
つまり \(x-\frac{1}{x}<0\)である。
以上から、答えは \(x-\frac{1}{x}=-\sqrt5\)
ここでよく
 生徒
生徒どうして \(0<x<1\) であるから \(x<\frac{1}{x}\) なの?
という疑問があがります。
どうして \(0<x<1\) のときに逆数をとると大小関係がひっくり返るのか?
実際に悩んでいる人も少なくないようです。
今回はそのことについてお話します。
- \(0<x<1\) であるから \(x<\frac{1}{x}\) となる理由が知りたい人
具体的な数字を代入してみる



まずは思いつく数字を代入してみて、本当に\(0<x<1\) のときに \(x<\frac{1}{x}\) となるのかを確かめてみましょう。
\(x=\frac{1}{2}\) としたら \(\frac{1}{x}\) はどうなりますか?
\(x=\frac{1}{2}\) のとき
$$\frac{1}{x}=\frac{1}{\frac{1}{2}}=\frac{2}{1}=2$$



\(x\) が \(\frac{1}{2}\) 、 \(\frac{1}{x}\) が \(2\) だから \(\frac{1}{x}\) の方が大きいですね。
これもたしかに \(x<\frac{1}{x}\) となります。
他の値でも確かめてみましょう。
\(x=\frac{1}{3}\) のとき
$$\frac{1}{x}=\frac{1}{\frac{1}{3}}=\frac{3}{1}=3$$



\(x\) が \(\frac{1}{3}\) 、 \(\frac{1}{x}\) が \(3\) だから \(\frac{1}{x}\) の方が大きいですね。
たしかに \(x<\frac{1}{x}\) となります。
\(x=0.1\) のとき
$$\frac{1}{x}=\frac{1}{0.1}=\frac{1}{\frac{1}{10}}=\frac{10}{1}=10$$



\(x\) が \(0.1\) 、 \(\frac{1}{x}\) が \(10\) だから \(\frac{1}{x}\) の方が大きいですね。
\(x\) が小数でも \(0<x<1\) ならたしかに \(x<\frac{1}{x}\) となります。



では、仮に \(0<x<1\) を満たさない \(x=5\) だとしたら?
\(x=5\) のとき
$$\frac{1}{x}=\frac{1}{5}$$



\(x\) が \(5\) 、 \(\frac{1}{x}\) が \(\frac{1}{5}\) だから \(x\) の方が大きいですね。
この場合は \(x<\frac{1}{x}\) とはなりません!
このように、ちゃんとした証明にはなっていませんが、具体的な値を代入することで直感的にどちらが大きいかを判断することができます。
\(0<x<1\) のときは \(x<\frac{1}{x}\) となる感覚がなんとなくでもわかったでしょうか?
次はもう少ししっかりと説明します。
グラフで考える



\(x\) と \(\frac{1}{x}\) の大小関係がわからないとのことなので、それぞれのグラフをかいて考えてみましょう。
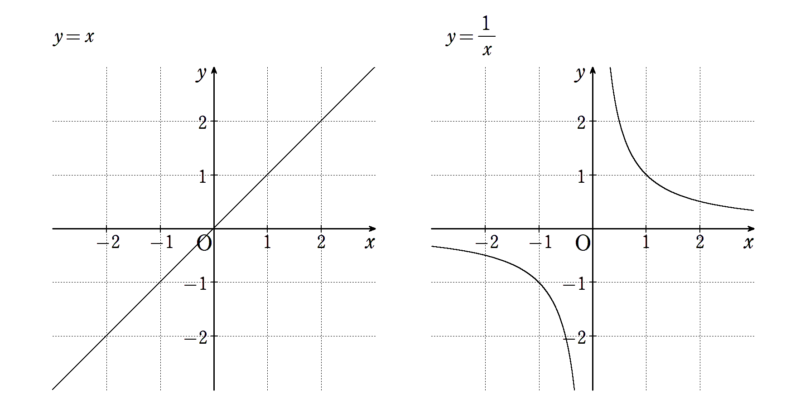

\(y=x\) は直線、 \(y=\frac{1}{x}\) は曲線(いわゆる反比例)のグラフになります。
この2つのグラフをまとめてみます。
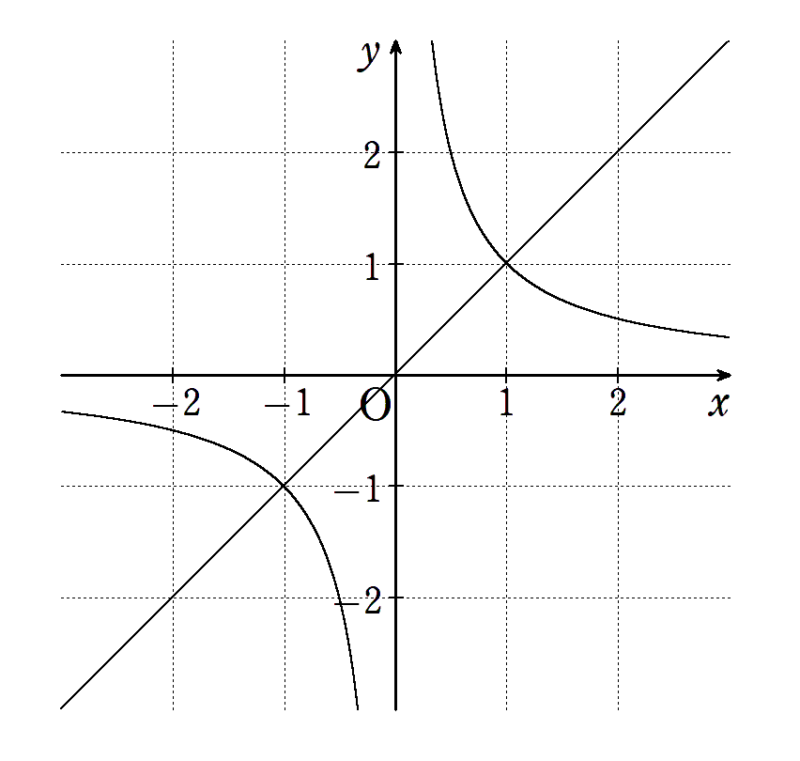




この図での \(0<x<1\) の部分がどこかわかりますか?
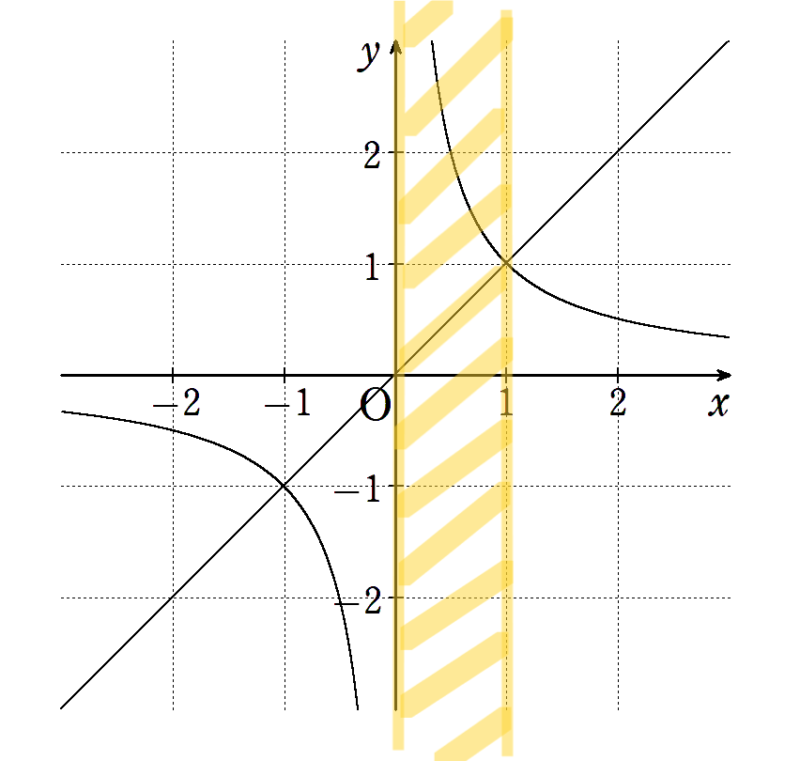

図の黄色いエリアが \(0<x<1\) になります。
解決したいのは、この範囲の中では\(y=x\) と \(y=\frac{1}{x}\) のどちらが大きいの?
ということです。



黄色のエリアの中では \(y=\frac{1}{x}\) の方が \(y=x\) より上にありますね。
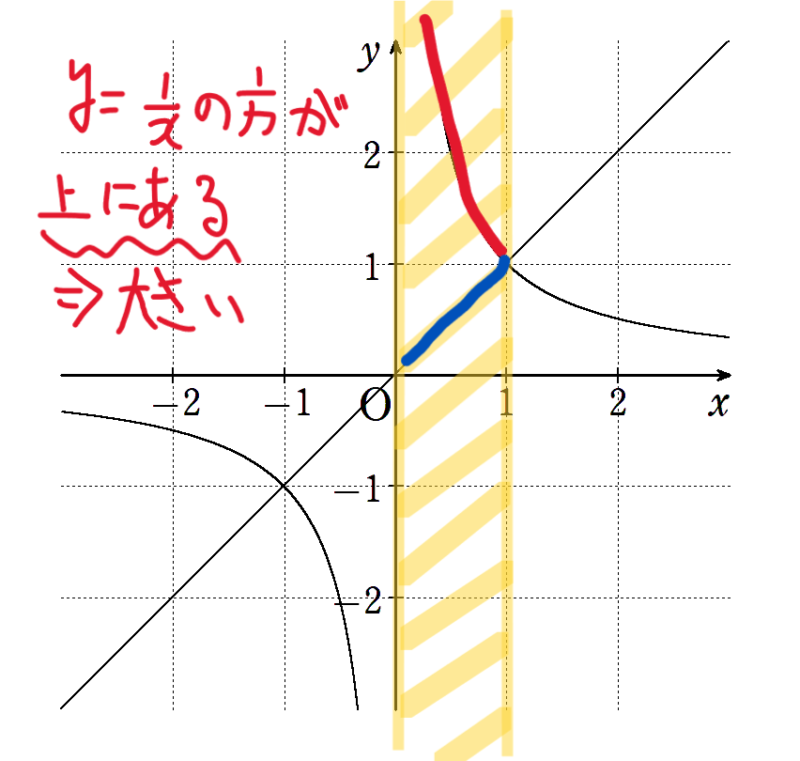

グラフAグラフBでAの方が上にあるときは、Aの方が大きい。
このことから、 \(0<x<1\) ( \(x\) が黄色いエリアにいる)のとき、 \(y=\frac{1}{x}\) の方が \(y=x\) より大きい。
つまり、 \(x<\frac{1}{x}\) といえます。
グラフの黄色いエリア以外を見ると
\(-1<x<0,1<x\) のときは \(x>\frac{1}{x}\)、
\(x<-1\) のときは \(x<\frac{1}{x}\) ということもわかります。
まとめ
\(x\) の値によって大小関係が変わるのは確かにややこしいです。
数Ⅰの範囲なので、看護の専門学校の受験を考えている人も理解しておかないといけません。


これは暗記するというよりは、わからなくなったら自分で調べることが重要です。
直感的に判断したい場合は具体的な値を代入すればよいですが、グラフの方でも判断できるようになっておきましょう。