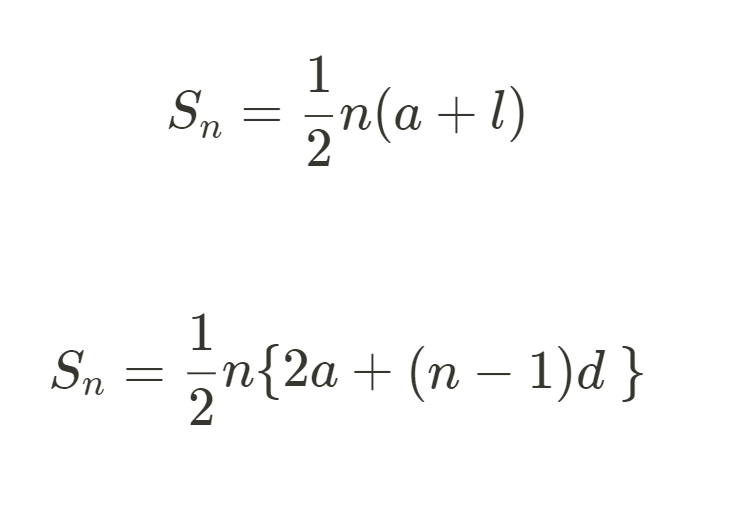等差数列の和の公式の成り立ちとおすすめ活用法を解説

等差数列の和の公式には２種類あります。

今回はそれぞれの成り立ちとどうやって使い分ければよいのか、その活用法を紹介します。

当てはまる人はぜひ読んでください。

等差数列の和の公式 \(S_n=\frac{1}{2}n(a+l) \) の成り立ちを考える

最初は

$$S_n=\frac{1}{2}n(a+l)$$

の成り立ちと活用法を学習しましょう。

なぜ、この公式を使えば等差数列の和が求められるのかを考えます。

具体例を用いて考えてみましょう。

1から10までの整数を足し合わせた数の和 \(S\) は？

これくらいなら小学生でも解くことができます。

$$S=1+2+3+4+…+10=55$$

電卓を使っても暗算で解いてもいいです。

答えは55です。

ではこの問題はどうでしょう。

1から100までの整数を足し合わせた数の和 \(S\) は？

暗算でやるのはキツイし、電卓を使ってもどこかで間違えそうです。

昔の人はこの問題を工夫して解きました。

それが以下の方法です。

---

まずは

\(S=1+2+3+4+……+100\)　… ①

のように ① とおいてしまいます。

次に、足し合わせる順番をひっくり返した式を ② とします。

\(S=100+99+98+97+……+1\)　… ②

① と ② はもちろん同じ意味です。

この ① と ② の左辺同士、右辺同士を足します。

\begin{array}{rr}
& S= 1+ 2+ 3+ 4+……+100\\
+\big{)}&S=100+99+98+97+……+1\\
\hline
&2S=101+101+101+101+……+101
\end{array}

左辺は求めたい \(S\) が ① と ② のどちらにもあるので、合わせて \(2S\) となります。

右辺ですが、縦のラインで見ると101が100個あるので、\(100\times101\)をします。

$$2S=100\cdot101$$

求めたい和は \(S\) なので、最後に2で割ります。

$$S=\frac{1}{2}\cdot100\cdot101=5050$$

---

めちゃくちゃ賢い解き方ですよね！

さて、ここで「101」とはどこから出てきた数字なのかを考えます。

つまり101 というのは、初項＋末項から求められます。

また、100 というのは「何個足し算をしているのか」を表した数なので、項数にあたります。

以上のことから、一般的な公式は

$$ S=\frac{1}{2}\times(項数)\times(初項+末項) $$

となります。

初項は「最初」という意味なので、アルファベットの最初の文字である \(a\)
末項は「最後」「last」の \(l\)
項数は「number」の \(n\) 　の略

例題

（１）初項3、末項19、項数15の等差数列の和を求めよ。
（２）初項1、公差3の等差数列の初項から第n項までの和を求めよ。

解説

（１）は等差数列の和の公式がそのまま使えます。

$$S=\frac{1}{2}\cdot15(3+19)$$$$=\frac{1}{2}\cdot15\cdot22$$$$=165$$

（２）は、ぱっと見だと末項が見当たらないので公式が使えません。

ここでさらに注目したいのが、「末項が第n項」であるということです。

末項を求めるために一般項を求める公式を使いましょう。

（一般項）=\(1+(n-1)\cdot3\)\(=3n-2\)

これで末項を求めることができたので、公式が使えます。

$$S=\frac{1}{2}n\lbrace1+(3n-2)\rbrace$$$$=\frac{1}{2}n(3n-1)$$

答え（１）165、（２）\(\frac{1}{2}n(3n-1)\)

等差数列の和の公式 \(S_n=\frac{1}{2}n \lbrace 2a+(n-1)d \rbrace\) の成り立ちを考える

続いて、

$$S_n=\frac{1}{2}n \lbrace 2a+(n-1)d \rbrace$$

の成り立ちと活用法を学習しましょう。

なぜ、この公式を使えば等差数列の和が求められるのかを考えます。

（２）初項1、公差3の等差数列の初項から第n項までの和を求めよ。

先程の問題を例に考えます。

これを解くために先程の学んだポイントを思い出します。

今回の問題では「一般項」と「第n項」と「末項」はすべて同じ意

初項 \(a\)、公差 \(d\) の等差数列の一般項 \(a_n\) を求める公式は

$$a_n=a+(n-1)d$$

ですので、末項 \(l\) を求める公式も

$$l=a+(n-1)d$$

ということになります。

これを等差数列の和の公式に当てはめてみましょう！

$$S_n=\frac{1}{2}n(a+l)$$$$=\frac{1}{2}n \lbrack a+ \lbrace a+(n-1)d \rbrace \rbrack$$$$=\frac{1}{2}n \lbrace 2a+ (n-1)d \rbrace$$

末項を使う公式を覚えていないとできないやり方ですが、逆に言えば1つ覚えてしまえばもう1つも覚えられるということです。

初項は「最初」という意味なので、アルファベットの最初の文字である \(a\)
公差は英語で「common difference」なので \(d\)
項数は「number」の \(n\)　の略

例題

では、改めて公式を使って問題を解いてみましょう。

初項1、公差3の等差数列の初項から第 \(n\) 項までの和 \(S_n\) を求めよ。

解説

初項、公差、項数のすべてがわかっているので、公式がそのまま使えます。

$$S=\frac{1}{2}n \lbrack 1+ \lbrace 1+(n-1) \cdot 3 \rbrace \rbrack$$$$=\frac{1}{2}n \lbrace 2+(n-1) \cdot 3 \rbrace$$$$=\frac{1}{2}n(3n-1)$$

答え　\(\frac{1}{2}n(3n-1)\)

扱った例題は、先ほど末項を使う公式の例題と同じでした。

つまり、1つの問題でも解き方は2パターンあるということです。

最後に、ちょっとだけ応用した問題を2つの公式を使って解いてみます。

ちょっとだけ応用問題

次の等差数列の和 \(S\) を求めよ。
$$12,15,18,…,99$$

実際の数列を見て、自分で必要な情報を抜き出す問題です。

この問題を2通りの解き方で解いてみようと思います。

公差を使う公式 \(S_n=\frac{1}{2}n \lbrace 2a+(n-1)d \rbrace\) で解く

公差を使う公式には初項、公差、項数が必要です。

ここで困ることは、項数は何？ということです。

こういうときは、他にわかる情報はないかを考えます。

一般項 \(a_n\) は

$$a_n=12+(n-1) \cdot 3$$$$=3n+9$$

これで一般項、つまり \(n\) 番目の数が \(3n+9\) ということがわかりました。

$$3n+9=99$$$$3n=90$$$$n=30$$

というわけで、公式 \(S_n=\frac{1}{2}n \lbrace 2a+(n-1)d \rbrace\) に当てはめてみましょう！

$$S=\frac{1}{2} \cdot 30 \lbrack 12+ \lbrace 12+(30-1) \cdot 3 \rbrace \rbrack$$$$=15 \lbrace 24+29 \cdot 3 \rbrace$$$$=15(24+87)$$$$=15 \cdot 111$$$$=1665$$

というわけで、答えは1665です。

答え　\(1665\)

末項を使う公式 \(S_n=\frac{1}{2}n(a+l)\) で解く

続いて、末項を使う公式で1665を導いてみましょう。

末項を使う公式には初項、末項、項数が必要です。

項数の30の求め方はさっきと同じなので省略します。

あとは末項ですが、これもすぐにわかりますね。

というわけで、公式 \(S_n=\frac{1}{2}n(a+l)\) に当てはめてみましょう！

$$S=\frac{1}{2} \cdot 30(12+99)$$$$=15 \cdot 111$$$$=1665$$

求められました。

項数を求める過程を省略したとはいえ、あっさりと解けましたね。

答え　\(1665\)

まとめ

今回は等差数列の和を求めるための2つの公式を学習しました。

どちらを使うにしても項数が必要ですが、一般項を求めれば項数もわかりましたね。

足りない情報は自分で求めることで、どちらの公式を使っても解くことができます。

末項を使う公式の方が覚えやすいし、途中計算も楽ですよね。

大抵の問題は \(S_n=\frac{1}{2}n(a+l)\) だけ知っていれば困りません。

末項が与えられていない問題も、一般項を求めることでわかるようになります。

つまり、とにかく困ったら

まずは一般項を求めろ！！

ということです。

もちろんどちらとも使える方が融通が利くのですが、1つでも覚えることを減らしたい！という人は \(S_n=\frac{1}{2}n(a+l)\) を使いこなすことに全力を尽くしましょう。